Babylonian Mathematics develops from the times of the early Sumerians to the fall of Babylon in 539 BC in Mesopotamia, and is especially known for the development of the Babylonian Numeral System

Image source: https://en.wikipedia.org/wiki/Babylonian_mathematics
What was math used for?
Sumerian mathematics developed probably as early as the 6th Millenium BC, as a response to bureaucratic needs for land measurement, taxation of individuals, etc. Furthermore, the Sumerians and Babylonians needed to describe rather large to chart the course of the night sky and develop the lunar calendar.
To make it easier to describe large numbers, the Sumerians were among the first to assign symbols to groups of objects. Starting from the 4th Millennium BCE, they began to use clay shapes of various sizes to represent different numerical values. To ensure that the numbers could be written with the same stylus used for the words of the text, these objects were replaced by cuneiform equivalents. Probably in Sumeria as early as 2700 – 2300 BCE, a rudimentary model of the abacus was in use.

Image source: https://search.creativecommons.org/photos/2aebfb8c-b616-4878-a849-408f1368f24c by matsuyuki
The numeric system
Sumerian and Babylonian mathematics was based on a sexagesimal number system, or base 60. The Babylonian numbers, unlike those of the Egyptians, Greeks, and Romans, in the left column the figures represented the largest values, as in the modern decimal system, but with base 60 and not 10. Furthermore, two distinct symbols were used to represent the numbers 1 – 59, a unit symbol (1) and a ten symbol (10) which were combined in a similar way to the familiar system of Roman numerals (e.g. 23 would be shown as 23). The number 60 was represented by the same symbol as the number 1 and, due to the lack of a comma, the actual positional value of a symbol often had to be inferred from the context.

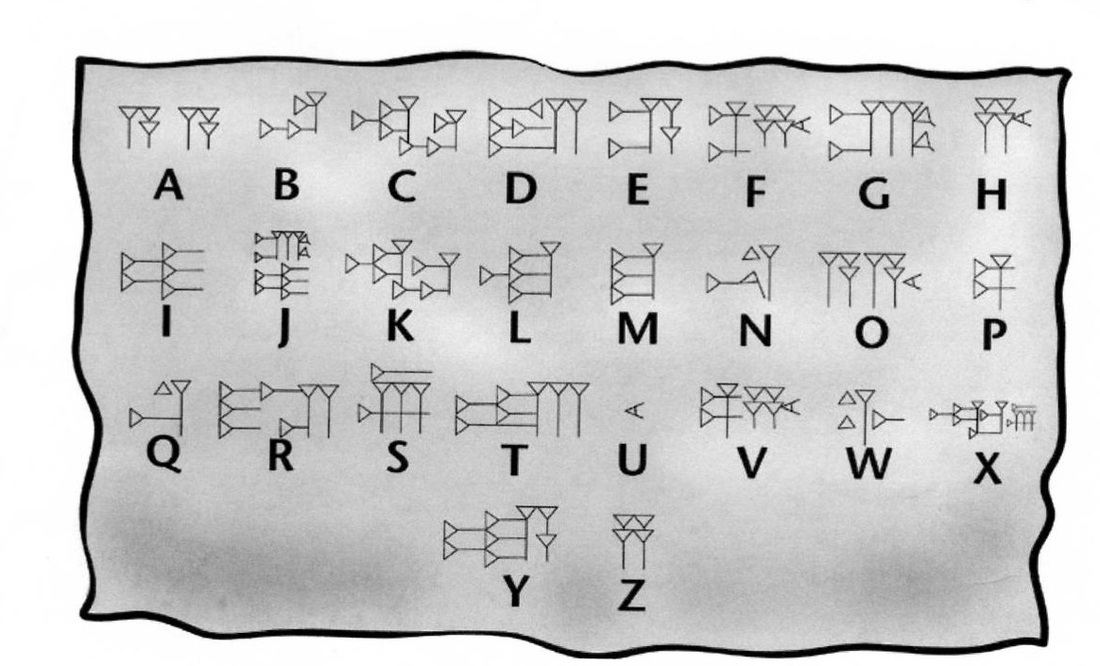

Images source: https://cte.univ-setif2.dz/moodle/mod/book/tool/print/index.php?id=15503
It has been speculated that Babylonian advances in mathematics were facilitated by the fact that 60 has many dividers and the continuous modern use of 60 seconds in a minute, 60 minutes in an hour, and 360 (60 x 6) degrees in a circle, are evidence of the ancient Babylonian system. It is for similar reasons that 12 has historically been a popular multiple (e.g. 12 inches, 12 months, 2 x 12 hours, 12 pence, etc). The Babylonians also developed a circular character for zero.
The use of a sexagesimal system was due to the Babylonians’ desire to develop accurate calendars both to track the change of seasons and to predict the best times for sowing. Initially, the Babylonians believed that there were 360 days in a year, and this formed the basis of their numerical system. Our entire system of geometry, astronomy, and dividing the day into seconds, minutes, and hours comes from this historical period.
Fractions
In the sexagesimal system, any fraction in which the denominator is a regular number (having only 2, 3, and 5 in its prime factorization) may be expressed exactly. The table below shows the sexagesimal representation of all fractions of this type in which the denominator is less than 60. The sexagesimal values in the table below may be interpreted as giving the number of minutes and seconds in a given fraction of an hour; for instance, 1/9 of an hour is 6 minutes and 40 seconds.
| Fraction: | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/8 | 1/9 | 1/10 |
|---|---|---|---|---|---|---|---|---|
| Sexagesimal: | 30 | 20 | 15 | 12 | 10 | 7,30 | 6,40 | 6 |
| Fraction: | 1/12 | 1/15 | 1/16 | 1/18 | 1/20 | 1/24 | 1/25 | 1/27 |
| Sexagesimal: | 5 | 4 | 3,45 | 3,20 | 3 | 2,30 | 2,24 | 2,13,20 |
| Fraction: | 1/30 | 1/32 | 1/36 | 1/40 | 1/45 | 1/48 | 1/50 | 1/54 |
| Sexagesimal: | 2 | 1,52,30 | 1,40 | 1,30 | 1,20 | 1,15 | 1,12 | 1,6,40 |
However numbers that are not regular form more complicated repeating fractions. For example:
1/7 = 0;8,34,17,8,34,17 … (with the sequence of sexagesimal digits 8,34,17 repeating infinitely many times) = 0;8,34,17
1/11 = 0;5,27,16,21,49
1/13 = 0;4,36,55,23
1/14 = 0;4,17,8,34
1/17 = 0;3,31,45,52,56,28,14,7
1/19 = 0;3,9,28,25,15,47,22,6,18,56,50,31,34,44,12,37,53,41
In arithmetic the two numbers 59 and 61, are both prime numbers implies that simple repeating fractions that repeat with a period of one or two sexagesimal digits can only have 59 or 61 as their denominators (1/59 = 0;1; 1/61 = 0;0,59), and that other non-regular primes have fractions that repeat with a longer period.
From numbers to geometry

Image source: https://search.creativecommons.org/photos/a57462ff-6c23-434c-8de1-ced59a8c0322 by cajut

Image source: https://search.creativecommons.org/photos/4aa5fbea-54da-4b00-b5b3-7d920668b3e0 by blondinrikard
The idea of square numbers and quadratic equations, where the unknown quantity is multiplied by itself, was born for the measurement of land, and the Babylonian mathematical tablets are the first proof of the solution of these equations. The Babylonian approach to solving them revolved around a geometric game in which shapes were sliced and rearranged. At least some of the examples found seem to indicate problem-solving for an end in itself rather than solving a concrete practical problem.
The Babylonians in their buildings, design and in gaming dice as well as backgammon, used geometric shapes. Their geometry included the calculation of the volumes of simple shapes such as cylinders and bricks, such as the areas of triangles, rectangles, and trapezoids.
The Plimpton 322 clay tablet (around 1800 BCE), indicates that the Babylonians may have recognized, that the square of the hypotenuse equals the sum of the square of the other two sides, centuries before Pythagoras. 15 perfect Pythagorean triangles with full sides are listed on the tablet, although some claim that they were simply exercises.

Image source: https://search.creativecommons.org/photos/3f54e035-1281-47ee-a370-25108add5adc by OliBac
Who inherited and developed this knowledge?
The Babylonians, Sumerians, and other inhabitants of the Euphrates valley developed the basis of numerical notation, arithmetic, and using fractions. Their work was adopted by the Greeks, who learned mathematical techniques. Alexander the Great after conquering the area along the Silk Route from Anatolia (Turkey) to China, sent astronomical documents from Babylonia to Aristotle. The Greeks began to explore the relationships between numbers.
Info sources:
https://en.wikipedia.org/wiki/Sexagesimal
